La page de Bernard Baudouin
Conception d’une réserve à soufflet
La page de Bernard Baudouin est devenue un blog à part entière:
http://o-d-b-selon-b-baudouin.blog4ever.com/
et le calcul des ressorts un article entier:
Bonne chance à Bernard!
un article sur l'adéquation des ressorts d'une soufflerie avec réserve en coin dont l'auteur Bernard Baudoin a rectifié le calcul en contournant la difficulté par des mesures empiriques plus faciles d'accès qu'un calcul complexe utilisant la trigonométrie qui rebute le constructeur moyen:
Pour fournir de l'air dans nos OdB (orgues de barbarie), les pompes actionnées par une manivelle envoient de l'air dans une "réserve" généralement en soufflet en forme de coin où la pression est maintenue par l'action d'un ressort qui appuie sur le battant de cette réserve.
Dans les orgues d'église, le principe est le même, à cela près que la pression dans la réserve est maintenue par l'action d'un poids (souvent une pierre).et que le soufflet est en forme de lanterne avec des pantographes qui maintiennent les faces parallèles.
L'objet de cet article porte sur cette différence: une pierre fournit une force constante (son poids) quelle que soit la position du soufflet de la réserve, alors qu'un ressort fournit une force qui dépend (quasi linéairement) de son élongation. Ce qui signifie qu'à chaque position du volet de la réserve correspond une pression différente.
Comment contourner cet écueil dans nos OdB ?
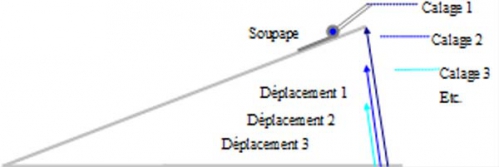
En fait, on met en place une soupape de décharge qui est conçue de telle manière que lorsque la réserve est "pleine", et risquerait d'éclater en position haute, la soupape s'ouvre et laisse passer l'air excédentaire fourni en continu par les soufflets d'alimentation. Le ressort fournit dans cette position, avec une élongation fixe, une force constante et donc une pression calculable et mesurable également constante.
On peut se maintenir dans cette position et donc obtenir que la soupape de décharge ne se ferme jamais, le débit d'air utilisé par les flûtes étant prélevé avant le débit de fuite de celle-ci.
Avec cette conception, le volume de la "réserve" n'est d'aucune importance puisqu'il reste toujours dans la même position.. Mais l’inconvénient c’est un bruit permanent de fuite à la soupape et un effort maximal et permanent.
Que faut-il pour que cette pression ne varie pas pendant la course du battant? Ou comment améliorer nos réserves à soufflet
La présente méthode vise à réaliser une réserve dont la pression interne resterait constante pendant tout le débattement du battant, moyennant quelques mesures et un calcul facile.
Le principal avantage de cette méthode permet de produire l’air en pression sans sur dimensionner les soufflets et donc de réduire au plus juste l’effort permanent et inutile à la manivelle à la moyenne de consommation plutôt que la consommation de pointe. La réserve joue alors un rôle d’écrêtement des pointes de consommations qui ne dépassent qu’occasionnellement la production de l’air moyenne.
Le principe de base : comprendre que la pression interne est due à la force avec laquelle le ressort appuie sur le battant, sachant que cette pression interne génère elle aussi des forces complexes exercées sur les éclisses en fonction de l’angle entre elles et fonction de la position du battant. Partant du principe qu’elles exercent des forces plus fortes en position vide et moins fortes en position pleine, cette différence peut être compensée exactement par les variations de force du ressort en fonction de son allongement si la raideur du ressort est correctement choisie.
Couples engendrés
Ces forces agissent selon la distance de leur point d’application avec le point d’articulation du volet (bras de levier). Les couples sont le produit de ces valeurs.
Couple = force x bras de levier
1 / Les forces dues à la pression interne sur les éclisses et le battant varient en fonction de la pression bien sûr, et de l’angle du battant avec le coté fixe, donc de l'angle correspondant des éclisses. Le bras de levier n'est pas facile à déterminer par le calcul, c'est pour cela que nous faisons des mesures contournant cette difficulté.
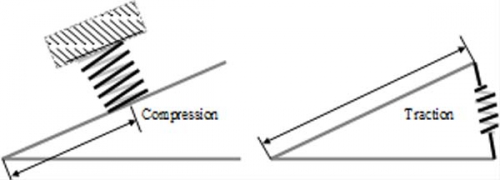
2 / La force générée par le ressort varie en fonction de l'élongation (ressort de traction) ou le raccourcissement (ressort de compression) de ce ressort. Le bras de levier est la distance entre le point d’articulation du volet et le point d’application (ou de pression) du ressort.
Si ce couple « ressort » est à tout instant égal – et opposé - au couple « pression » évoqué plus haut, la pression interne restera constante pendant toute la phase d’utilisation de la réserve.
Plutôt que calculer ces valeurs par des formules complexes il est plus facile de mesurer empiriquement les pressions et les efforts en suivant la méthode utilisée ci après.
A Mesure des caractéristiques du ressort utilisé.
Pour les unités, il est préférable pour ne pas s'emmêler de noter les forces en Newtons (on peut adopter 1 Kg = 10 N. ; si on voulait être très rigoureux, il faudrait prendre 1 Kg = 9,81 N, mais ce n'est pas utile dans le cas présent).
Méthodes :
Pour un ressort de traction, il suffit d'accrocher le ressort à une potence, de suspendre des poids à l'autre extrémité, et de mesurer la longueur du ressort résultante.(Ne pas inclure les boucles dans cette mesure).
Pour un ressort de compression, il faudra peut-être réaliser un bâti pour éviter que le ressort ne « flambe ». Une planchette avec charnière peut convenir. Attention dans ce cas à minimiser ou tenir compte des effets de levier éventuels qui risquent de perturber la mesure. Il faut mettre les poids bien en face de l'appui du ressort. Il faut se débrouiller aussi pour que l'axe du ressort reste vertical, ou plutôt que le poids agisse bien verticalement à chaque mesure, pour que la force relevée soit bien celle dudit poids, et non pas son cosinus.
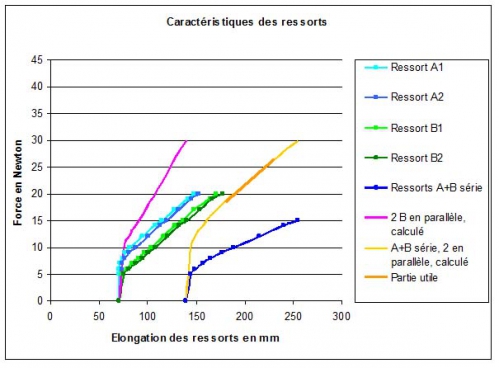
Nous aurons deux séries de chiffres par ressort, à partir desquels nous pourrons construire les diagrammes force /élongation.
Pour illustrer le propos, voici les valeurs obtenues avec le matériel (ressorts de traction) dont je dispose :
B Mesure de la courbe : pression délivrée en fonction du déplacement du volet mobile.
Méthode :
Tout étant en place pour le fonctionnement normal de la soufflerie, ajuster le niveau de la butée de la soupape de décharge à différentes valeurs, pour obtenir différentes positions du volet mobile.
Noter les valeurs de pressions obtenues au pèse-vent, et les positions de volet mobile correspondantes. ( On peut brancher le pèse-vent sur une embase de flûte retirée, et scotcher la flûte de Pan en laissant libre cette note )
Construire soigneusement un diagramme des valeurs obtenues.
Exemple : Valeurs obtenues avec deux combinaisons de ressorts
Au passage, avec ces ressorts non optimisés, on observe a priori une pression différente pour chaque position du volet mobile,
C Mesure du bras de levier d'action du ressort.
C'est la distance entre le point d'application de la force du ressort, et l'articulation du volet mobile.
Pour ne pas s'emmêler, il est préférable de l'exprimer en mètres.
Nous pouvons construire avec soin un diagramme : couple du ressort en fonction du débattement du volet mobile.
Le couple est le produit force du ressort x bras de levier, pour chaque débattement du volet mobile et donc chaque longueur du ressort.
Dans mon exemple, le bras de levier est de 0,36 m.
D Calcul des caractéristiques de la réserve en essai.
Nous allons calculer des « coefficients » caractérisant la réserve en essai, qui, étant le résultat de mesures réelles, incluent l'effet des éclisses quelles que soient leur forme.
Il suffit pour chaque position du volet, de diviser le couple ressort correspondant, par la pression mesurée dans cette position. Ces valeurs sont tirées des diagrammes construits ci-dessus
En fait, les variations étant linéaires (ou quasi), il suffit de faire ce calcul pour les positions hautes et basses du volet mobile.
Nommons ces résultats Coeff.(maxi) et Coeff.(mini) pour respectivement les positions haute et basses du volet mobile.
Exemples avec mon matériel :
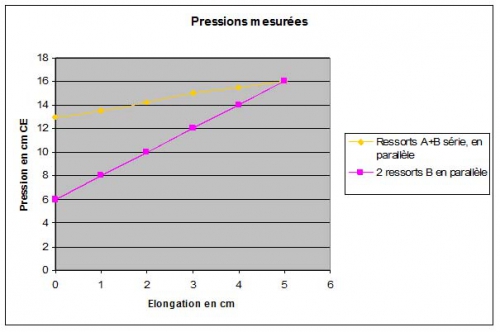
Ressorts A+B série, deux en parallèle
Coeff.(maxi) = 9,5 N.m / 16 cm CE = 0,594
Coeff.(mini) = 6,7 N.m / 13 cm CE = 0,515
Deux ressorts B, en parallèle
Coeff.(maxi) = 9,7 N.m / 16 cm CE = 0,606
Coeff.(mini) = 2,9 N.m / 6 cm CE = 0,483
On voit qu'avec différents ressorts, les coefficients sont quasiment identiques. Ils caractérisent seulement les dimensions géométriques de la réserve utilisée.
On pourra adopter pour caractériser CE MATERIEL: Coeff.(maxi) = 0, 6 et Coeff.(mini) = 0,5 . Vos coefficients seront à priori différents.
E Calcul du ressort optimum.
A ce stade, nous sommes maîtres de décider de la pression de fonctionnement souhaitée.Dans ces conditions, les forces à demander au ressort sont :
Force maxi. = Coeff.(maxi) x Pression / Bras de levier ressort
Force mini. = Coeff.(mini) x Pression / Bras de levier ressort
Et la raideur à exiger est :
(Force maxi - Force mini ) / Variation de longueur correspondante
Soit pour l'exemple considéré et le choix de 14 cm CE:
Pour d = 0 , force minimale :
0,5 x 14 / 0,36 = 19,4 N
( Pour un ressort quel qu'il soit, la force minimale est obtenue par son allongement ou sa compression au « repos » )
Pour d = 5 , force maximale :
0,6 x 14 / 0,36 = 23,3 N
Raideur ( 23,3 N - 19,4 N ) / 5 cm de débattement réel = 0,78 N/cm
Surtout éviter Le site de Vanel qui est catastrophique dans toute la chaine de la commande à la livraison et la facturation!!
Et faire une « recherche avancée » dans les ressorts de traction ou de compression où on pourra utiliser les données ci-dessus.
Vous y trouverez même des indications (diamètre de la corde à piano, diamètre du ressort, nombre de spires, etc) si vous voulez tenter de bricoler vos ressorts vous même, sans garantie du résultat !. C'est à mon avis une option plus chère que de commander le bon ressort.
Attention : il faut se souvenir que deux ressorts identiques mis en parallèle (pour augmenter la force résultante) voient leurs raideurs s’ajouter.
Pour mon exemple, je trouve qu'avec deux éléments en parallèle (configuration de ma soufflerie oblige), la référence U. 111.070.0450.AX conviendrait.
Vue des ressorts d'essai en série.
Le même montage est installé symétriquement de l'autre coté des soufflets
Pour toute question complémentaire Bernard Baudouin se fera une joie de vous répondre sur:
Vous y trouverez toutes ses astuces et calculs pour réguler la pression d'une réserve et plein d'autres choses comme les pertes de charges et les calculs de débits...
Nous lui souhaitons bonne chance!
Bernard Baudouin nous a produit d'autres contributions sur le débit des soufflets:
Mais aussi sur le débit et la vitesse de sortie de l'air dans les lumières ou les pertes de charges dans les flûtes.
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 353 autres membres