L'orgue de barbarie de Bernard et Philippe

1) Avant la lumière (et seulement dans les tuyaux en bois)

Dans les calculs de  nos diapasons le paramètre vitesse de sortie de l'air à la sortie de la lumière est calculée avec des lois connues et largement admises sans remise en cause. comme la loi de Bernoulli. Elle est présente dans les paramètres de construction comme une constante commune à l'ensemble des flûtes au même titre que le nombre d'Ising ou la pression.

Cette vitesse se déduit du calcul selon la loi de Bernoulli:

où :

${\displaystyle p\,}$ est la pression en un point (en Pa ou N/m²)

${\displaystyle \rho \,}$ est la masse volumique en un point (en kg/m³)

${\displaystyle v\,}$ est la vitesse du fluide en un point (en m/s)

${\displaystyle g\,}$ est l'accélération de la pesanteur (en N/kg ou m/s²)

${\displaystyle z\,}$ est l'altitude (en m)

 Nota: On commence par négliger la compressibilité du gaz et la variation g.z ...

Ce qui donne une vitesse uniforme pour l'ensemble des flûtes d'un même jeu. Ce calcul parce qu'il est simplificateur est uniformément admis sans remise en cause. Il devient alors source d'approximations et d'erreurs dans la plus part des calculs qui en découlent.

La dynamique des fluides nous indique les corrections à apporter sur cette vitesse de sortie de l'air en lumière en fonction de trois autres paramètres comme les couches limites et de l'effet Venturi, mais aussi le diamètre de l'alimentation en pied:

• V air (m/s) : vitesse de la lame d’air dans un conduit calculée à partir du paramètre suivant par la formule de Bernoulli dont on sait qu’elle est différente pour les basses et les aiguës en raison de l' application des propriétés des couches limites. De plus la loi de poiseuille distingue déjà deux cas en fonction d'autres paramètres selon que le régime est laminaire ou turbulent. Puis il y existe deux régimes turbulents le lisse et le rugueux...
  

De plus les équations sont bien plus complexes pour la vitesse entre deux plaques comme dans le couloir entre le noyau et la lèvre inférieure:

 Équation du profil de vitesse où la vitesse maximale (au milieu de la couche) est fonction du gradient de pression, de la viscosité dynamique et de la distance entre les plaques : ${\displaystyle v_{\rm {max}}=-{\frac {h^{2}}{8\;\eta }}\;{\frac {{\rm {d}}p}{{\rm {d}}x}}}$

 .

• Pression (en cm d’eau) : La pression mesurée au  pèse-vent et uniquement dans la réserve est la même pour toutes mais sachant qu’elle doit être diminuée des pertes de charge dans les soupapes ou vannes et des gravures ou tuyaux et coudes de raccordement, elle est donc différente à la sortie de chaque chambre de noyau.

(Les pertes de charge dans les vannes peuvent être minimisées en utilisant la technique des chanfreins dans les vannes à membrane.)

 NOTA:

La pression dans chaque pied de flûte est aussi influencée par l'effet venturi du fait que chaque chambre de noyau est différente et plus importante pour les basses. Cette pression et par conséquent la vitesse de sortie du paragraphe précédent devraient être aussi calculées avec des résultats intermédiaires pour chaque flûte car elles influencent la vitesse de sortie et la hauteur de bouche . Encore des modifications à prévoir et à intégrer.

D'où l'utilité des flûtes à  hauteur de bouche réglable et lumière réglable.

• L'alimentation en pied de flûte : Le calcul du diamètre d’alimentation est fonction de la  consommation de chaque flûte.

Pour mémoire dans les diapasons de ce blog la section d'alimentation des flûtes est simplement proportionnelle à 6 fois celle de la lumière, plus exactement entre 5 et 7 fois...

Cette disposition est totalement empirique mais procure un bon équilibre de puissance sonore entre les aiguës et les basses.

le rapport fréquence pression

C'est là que j'ai trouvé la relation suivante page 16  §3.4 formule 3.8 qui montre la relation entre la lumière, la section d'alimentation, la pression et la vitesse de sortie du vent (voir aussi l'annexe E page 31).

On est donc très loin d'un calcul simple avec une vitesse uniforme pour l’ensemble d’un jeu!

D'ailleurs pour mémoire cette loi ne s'applique que dans le conduit avant la sortie juste avant la lumière!

 Le LAM (laboratoire d'acoustique musicale) nous explique les phénomènes en action à la sortie de la lumière:

 Vitesse de l'air à la sortie de la lumière

Pour assurer le bon fonctionnement d'un tuyau d'orgue il faut pouvoir régler indépendamment la quantité d'air sortant de la lumière (débit) et la vitesse d'écoulement de cet air.
La quantité détermine l'intensité du son.
Quand on agrandit le trou du pied, la pression monte à l'intérieur du pied. A la lumière, le débit et la vitesse de l'air augmente.
Quand on augmente la section de la lumière, la pression baisse à l'intérieur du pied, la vitesse de l'air diminue à la lumière mais le débit ne diminue pas.
En agissant sur la lumière on obtient des effets plus compliqués qu'en agissant sur l'ouverture du pied.

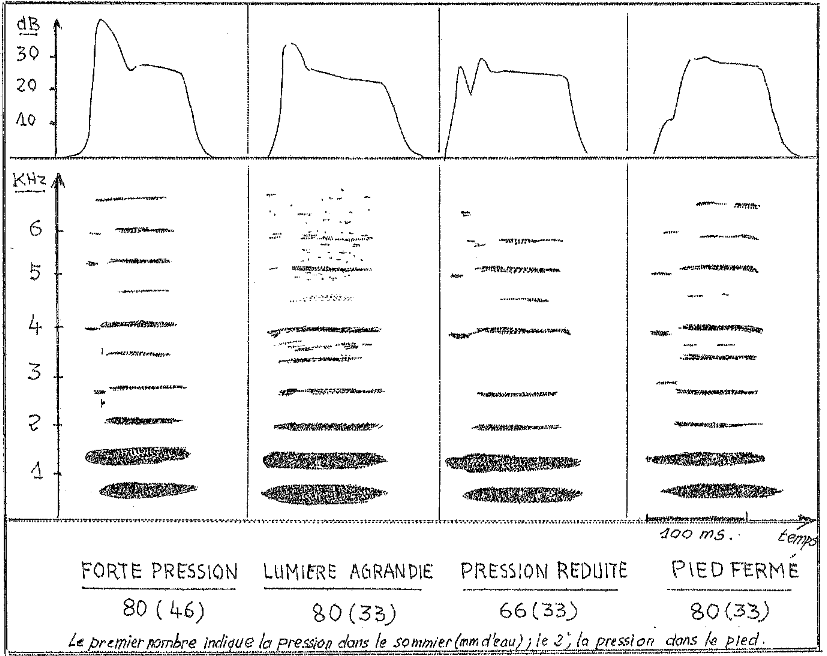
Fermer le pied a un effet identique à baisser la pression dans le sommier de l'orgue. L'intensité est plus faible, l'attaque est molle, les harmoniques supérieurs apparaissent avec un retard notable.

Agrandir la lumière diminue le retard du fondamental, les sons de bouche disparaissent et l'attaque est plus nette. Il y a un peu de bruit d'écoulement que l'on ne perçoit plus à quelques mètres de distance.

On peut obtenir la même pression dans le pied du tuyau soit avec une forte pression dans la gravure et un pied très fermé, soit avec une faible pression dans la gravure et le pied du tuyau grand ouvert.
Du choix de départ dépend un certain nombre de dispositions et le résultat esthétique n'est pas le même.

Exemple du "Plein-Vent":

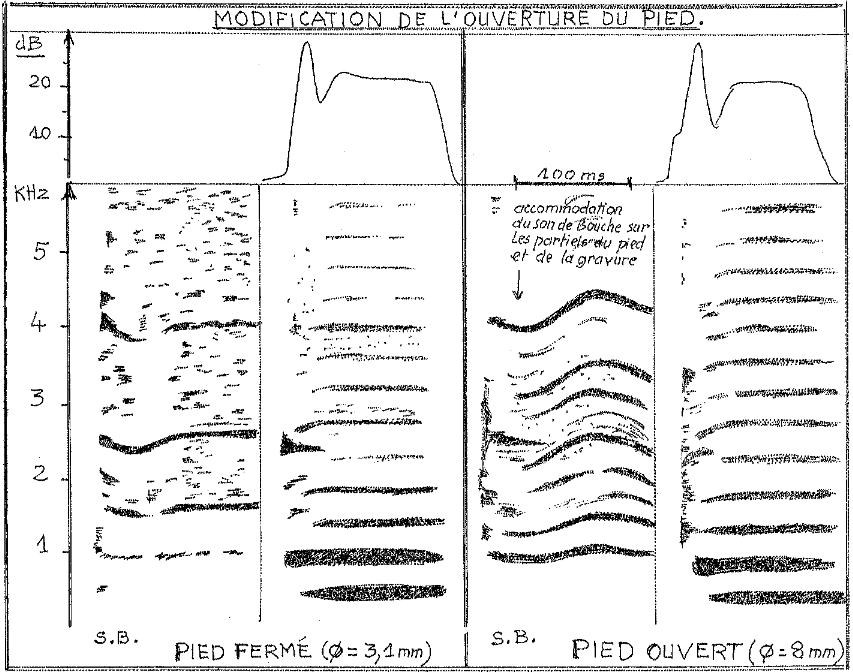
Prenons l'exemple d'un tuyau dont le pied est fermé et qui parle bien à pression élevée dans la gravure (*); si on ouvre le pied et que l'on baisse la pression dans la gravure afin que la pression dans le pied soit la même, l'attaque est très nette et le spectre, plus riche, est influencé par les partiels de la gravure, ce qui ne se produit pas pied fermé.
Il en résulte que l'harmonisation "plein vent" est plus délicate car il faut tenir compte des réactions de la gravure et des tuyaux les uns sur les autres. De plus on se prive de la possibilité de réglage au pied.
En revanche l'orgue a une sonorité particulière due à l'attaque franche des tuyaux, à leur grande richesse en harmoniques aigus, à leur fusion plus intime. Les fluctuations de pression sont plus perceptibles et peuvent donner plus de vie au son (légère instabilité de fréquence), si elles sont bien dosées.
(*) La "gravure", dans le sommier de l'orgue, est le couloir qui conduit l'air depuis la soupape jusqu'aux trous de la table, sous les tuyaux. La pression de l'air y est celle délivrée par la soufflerie. 

C'est ce que tente de prendre en compte la méthode de l’harmonisation par réglage en lumière en tâtonnant autour d'une position d'équilibre instable en jouant simultanément sur l'ensemble de ces paramètres.

Comme on peut le constater chaque paramètre influence simultanément plusieurs autres et les conséquences sont donc beaucoup plus complexes que ce que chaque loi théorique qui ne s'applique qu'à une seule variable prise isolément peut nous permettre de prévoir!

Pour prendre en compte l'interdépendance de ces paramètres dans mes diapasons pour chacun des paramètres (vitesse de sortie de l'air, pression, diamètre d'alimentation, dimension de la lumière) je recherche à mettre au point une méthode de calcul avec référence circulaire dans le tableau, ce qui  génère des calculs en boucle infinies si la fonction n'est pas convergente.

En revanche si la fonction est convergente il faut arrêter le calcul dès qu'une précision inférieure à une valeur prédéfinie choisie est atteinte pour limiter le nombre de boucles donc le temps de calcul.

Et ce n'est pas encore le cas actuellement mais on va s'y pencher!

2) Après la lumière (et pour tous les types de tuyaux)

Après les conditions sont totalement différentes le flux d'air qui sort de la lumière quitte une partie entre deux parois avec une vitesse importante et donc une pression très inférieure à la pression de départ déjà diminuée des pertes de charge.

La lumière est une interface entre deux mondes de natures différentes qui n'obéissent pas aux mêmes lois physiques.

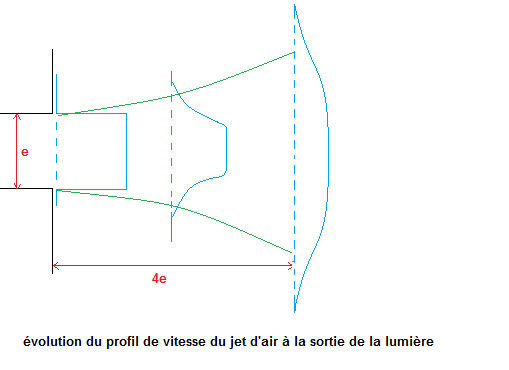
Dès la sortie de la lumière, le jet d'air est fortement freiné et dispersé par le changement brusque de pression et la viscosité de l'air ambiant, il se transforme en vortex.

Après une distance d'environ 3 à 4 fois l'épaisseur de la lumière la vitesse a déjà diminué de moitié et le profil s'élargit en s'aplatissant.

Source: The physics of musical instruments de  Neville H. Fletcher  2° édition page 509

J'y  rajoute la notion de distance selon les proportions du dessin qui je l'espère sont proportionnelles (ce que je ne peux vérifier actuellement)...

Pour la suite on peut se servir des données du site de Reiner Janke.

Ce qui montre par l'observation et des mesures physiques que la vitesse de l'air entre la sortie de lumière et le bord de la lèvre supérieure n'est même pas constante pour une flûte et une pression donnée!

la partie entre la fente de la lumière et une distance de 3 à 4 fois l'épaisseur de la lumière n'est ni affichée ni étudiée dans cette animation.

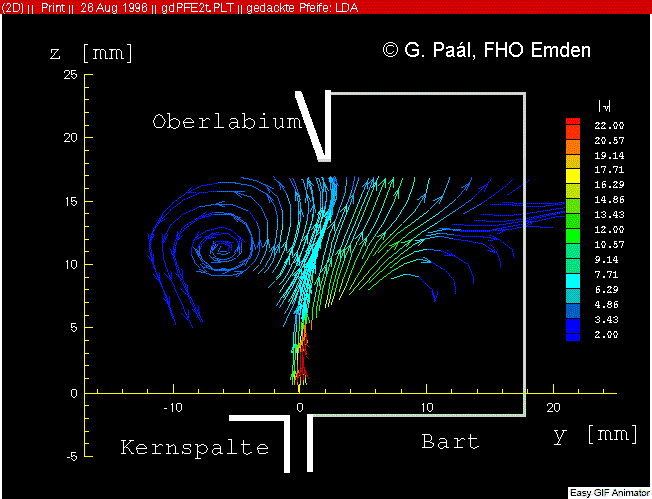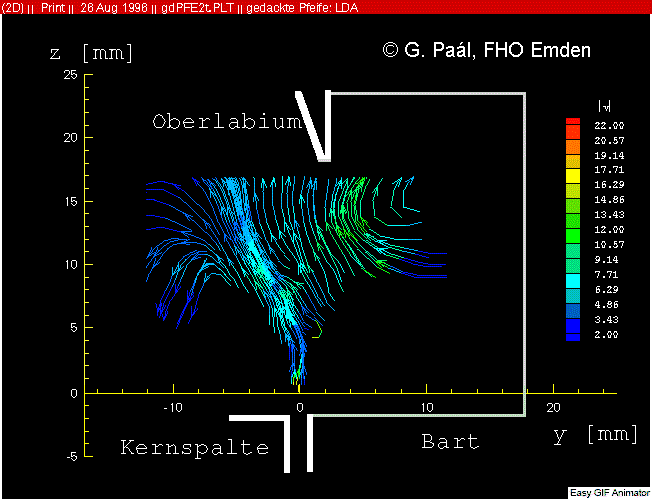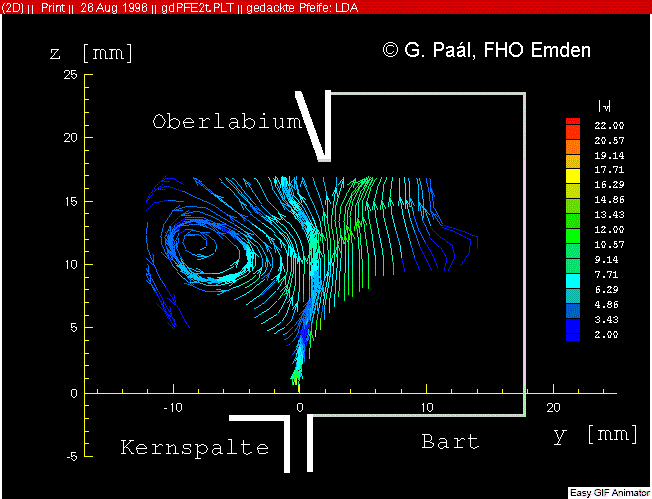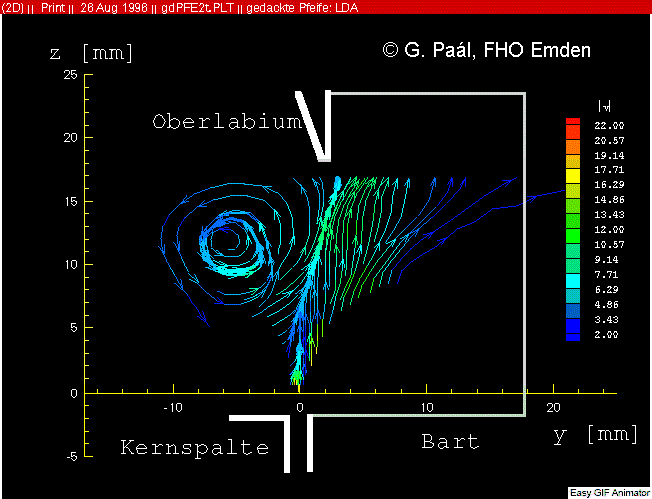
Mais cette animation nous confirme que le vortex passe plus de temps en dehors du corps qu'en dedans comme expliqué dans l'article ondes et pulsations.

Cette animation montre aussi que la vitesse après la sortie de lumière varie entre chaque oscillation entre 7 et 22 m/s (en observant la couleur en sortie de lumière) mais sur une courte distance. Sur le parcours jusqu'à la lèvre supérieure cette vitesse moyenne dans le jet est plus régulière et proche des 7 m/s ceci est très éloigné des 40 à 42 m/s qui sont pris en compte dans les diapasons pour une pression de 11 à 13 cm d'eau. L'auteur de l'article affirme que cette vitesse augmente principalement lorsque le vortex est à l'intérieur du corps de flûte.

Personnellement je pensais que cette "vibration" après la lumière était due au volume de la chambre du noyau qui joue un rôle identique au corps résonant et semble influencer non pas la fréquence mais la pression dans le noyau. De plus il y a un déphasage dans sa périodicité...

Ce phénomène est beaucoup plus connu et étudié avec le volume de la gravure pour les anches qui en général n'ont pas de résonateur et qui exigent bien un certain volume après l'anche mais avant la sortie de la lame de l'anche!

Ce phénomène est mieux expliqué par PP   sur son site mais comme toujours avec des incertitudes dont voici l'extrait donné à l'occasion de la construction de son 529 avec flutes et anches:

"Faire jouer les anches
Un véritable problème à part entière qui m'a occupé un bon moment, c'est peu de le dire !

Ce qui n'a pas fonctionné
Comme je l'ai dit au moment de la fabrication de ce registre d'anches, quand on souffle avec la bouche dans cette sorte d'harmonica géant, tout fonctionne à la perfection. Mais hélas dès qu'on y apporte de l'air via une canalisation d'un sommier, quelques anches seulement veulent bien sonner. Il suffit d'intercaler un tronçon de 5 ou 6 cm de tube avant le sommier des anches, pour que même avec la bouche, très peu d'anches fonctionnent.
Wouah !
Alors j'en ai essayé des trucs et des trucs ! Des cavités plus ou moins grandes sous les anches, des interventions à peine qualifiables sur les lames elle-même (heureusement que j'avais du rab), des anches différentes (j'ai même essayé du plastique), des sommiers de différentes épaisseurs et matières, des parois de sommier qui étaient censées vibrer... Bref, j'en passe et des plus saugrenues, mais à chaque fois que dalle ! Fonctionnement erratique et rien de bon.

Eureka !
Et puis à force de tripoter les choses dans tous les sens (si !) je me suis rendu compte qu'en ajoutant une cavité accordable après l'anche dans le sens du trajet de l'air, on résout tous les problèmes d'un seul coup. ET CA MARCHE :
- Quelque soit la pression. A moi les anches fortes ou pas fortes.
- Quelque soit l'orientation de l'anche. On peut souffler du côté du rivet ou de l'autre, ça marche de la même manière.
- Et avec une grande tolérance sur l'écartement de la lamelle par rapport au chassis. Pas besoin de l'adapter au contexte.
On prend les anches telles qu'elles sont, on pose et ça sonne. Que demander de mieux.

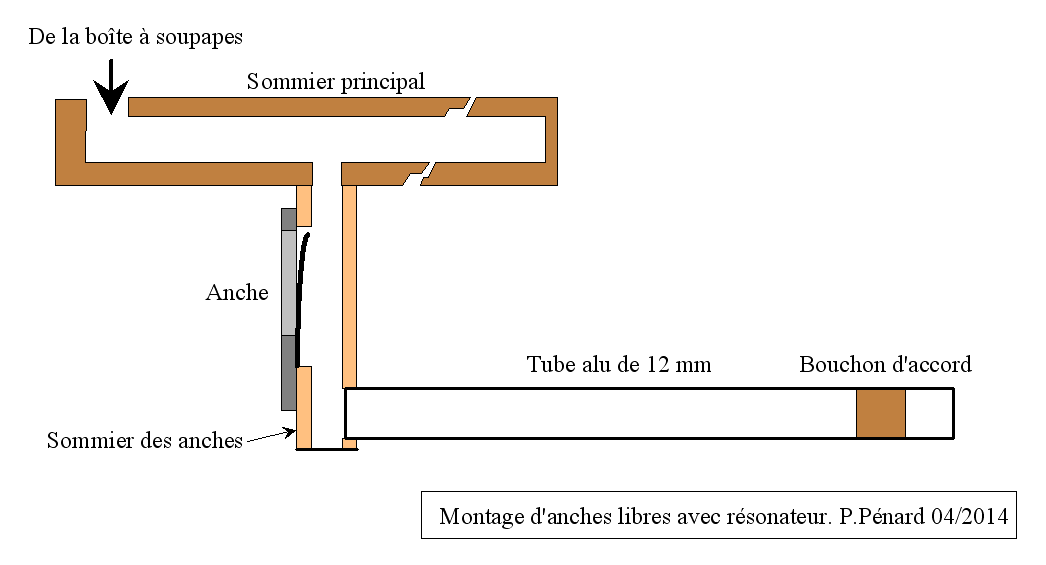
Au point où j'en étais de la compréhension de ce qui se passe, le dimensionnement de cette cavité a été purement expérimental :
- Je pars d'un tube avec un bouchon coulissant réglé au volume minimal dans un premier temps.
- On amène de l'air. Bien évidemment l'anche récalcitrante ne bronche pas ou fait un bruit bizarre.
- Et on tire doucement le bouchon pour augmenter le volume.
- A un moment c'est quasiment magique : l'anche se met à sonner, fort et clair.
- On note la position et on met à la place un tube bouché coupé à la bonne longueur. Ca sonnera désormais à tous les coups."

Mon article sur les pertes de charge 

les contributions de Bernard Baudouin au problème:

notion de pertes de charge

débits consommés par les flûtes

débits fournis par les soufflets